Gauss Elimination Method Problems 1 Solve the following system of equations using Gauss elimination method x y z = 9 2x 5y 7z = 52 2x y – z = 0 2 Solve the following linear The elimination method combines the following the multiplicative property of equality the additive property of equality Consider the pair of equations 2 x – y = 4 (Eqtn 1) x 1 theabhisheksingh0216 Answer 2xy=10 2xy=2 By solving these 2 equations, we get 4x=12 x=12/4 x= 3 by putting in any of the above equations 2xy=10 2 (3)y= 10 y= 106 y
Solved Find The Common Solution Of Each Using The Elimination Course Hero
2x+x-y/6=2 x-2x+y/3=1 by elimination method
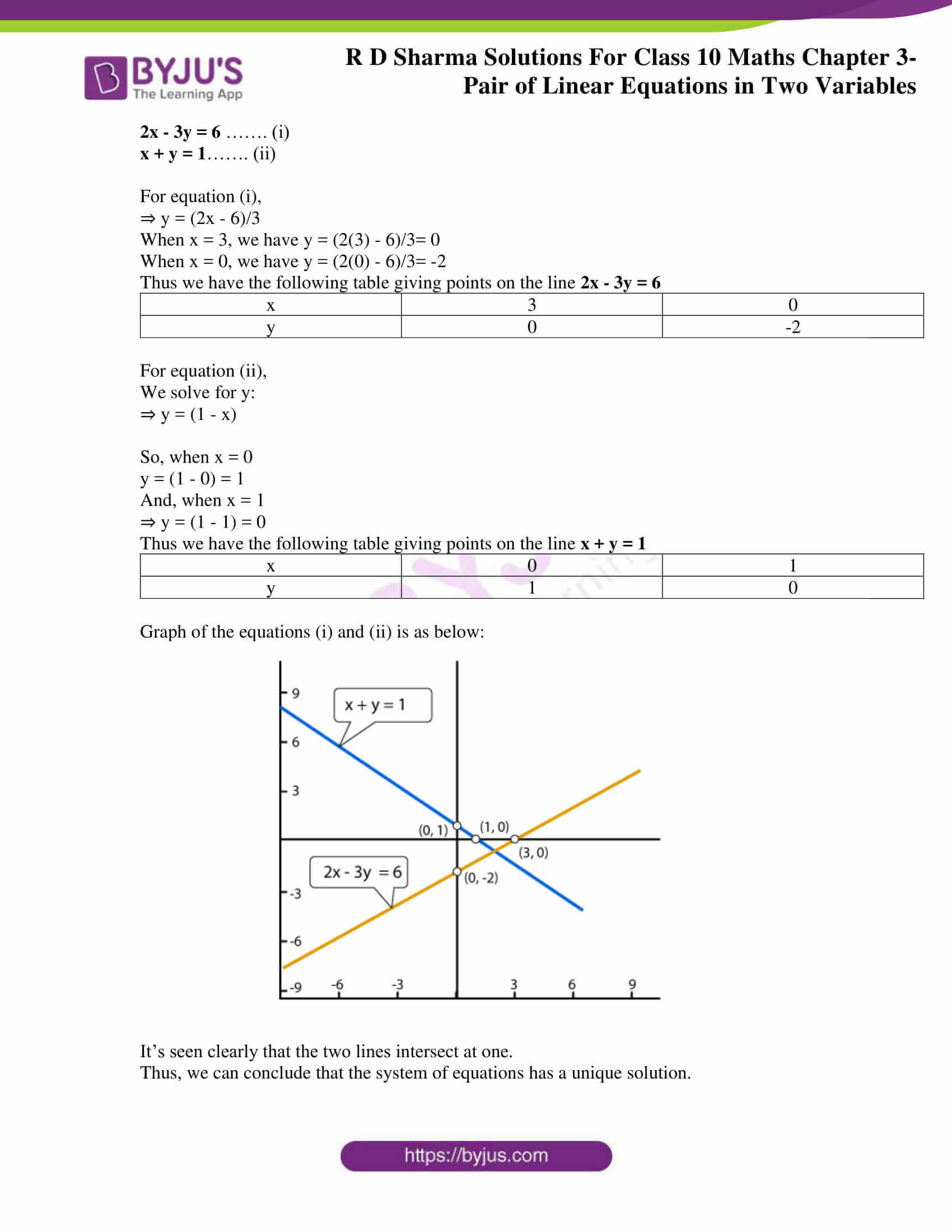
2x+x-y/6=2 x-2x+y/3=1 by elimination method-Solve the following systems of linear equations by Gaussian elimination method The last matrix is in row echelon form The corresponding reduced system is In (3), solve for z Divide bothNone of these eCan't be determined solve using elimination methodxy=1;2x3y=11 In what ratio is the segment joining the points (5,1), (3,5) divided by xaxis arrow left arrow left
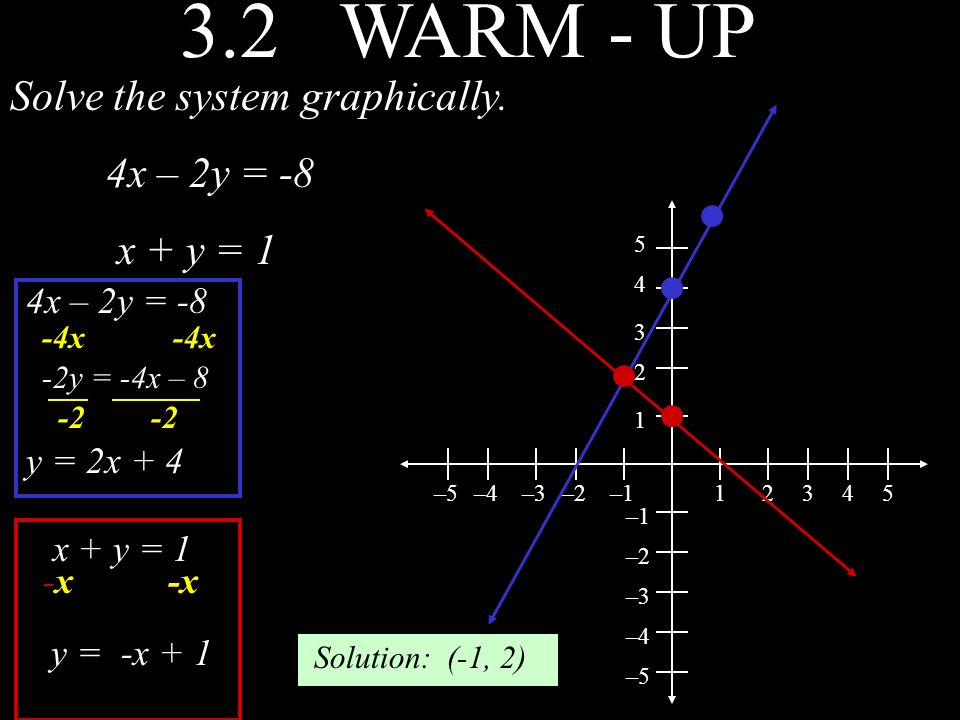



3 2 Warm Up Solve The System Graphically 4x 2y 8 X Y 1 5 4 3 2 5 4 3 2 X 2y 8 4x 2y 4x 8 Y 2x 4 X Ppt Download
Answer please thanks 1 Solve this system of equations using Gaussian Elimination 3x 4y – z = 6 2y 10z = 8 4y – 2z = 2 2 Solve the linear system by Gaussian elimination x y 2z w = Example Line 1 2x y = 6 Line 2 6x 2y = 4 Substitution Method This method involves isolating for one variable (x/y) of Line 1 then substituting that variable into Line 2 ThisUse the method of elimination to solve the system of linear equations given by Solution to Example 6 Multiply all terms in the first equation by 2 to obtain an equivalent system given by
When adding these equations together the x terms are added to the x terms , the y terms are added to the y terms and the constant is added to the constant so you would have xx, which equalsIn the second question , first i swapped the y and the 7 after that i subtracted the first equasion from the second one the y cancels out cause its yy (equal to zero) , the 2x3x becomes x Explanation Subtracting equations, x − 2x = 2 − − 1 −x = 3 x = − 3 y = 2 −x = 2 − −3 = 5 Check −3 5 = 2 √
Answer 50 /5 BackPacker99 In order to eliminate x, we need it to make it equal to the inverse of 2x, which is 2x So, you could multiply y = x 4 by 2 to eliminate x Still stuck?Solve the system shown below using the Gauss Jordan Elimination method x 2 y = 4 x – 2 y = 6 Solution Let's write the augmented matrix of the system of equations 1 2 4 1 – 2 6 Now, weSolve the following system of linear equations by elimination method x (y/2) = 4 and (x/3) 2 y = 5 Solution 2x y = 8 (1) x 6y = 15 (2) In order to make the coefficient of x




Solved 3 58 Solve The System By Using The Elimination Chegg Com




Solve By Elimination Method X Y 6 X Y 4 Maths Linear Equations In Two Variables Meritnation Com
Add the two equations together to eliminate x x from the system Divide each term by 2 2 and simplify Tap for more steps y = −1 y = 1 Substitute the value found for y y into one of theThis is an example where we have to multiply both equations by some numbers such that when we add them either the xterms or yterms are eliminated If we want to eliminate the xterms,Example (Click to try) xy=5;x2y=7 Try it now Enter your equations separated by a comma in the box, and press Calculate!




Solve For X And Y X 1 2 Y 1 3 9 And X 1 3 Y 1 2 8 Brainly In




Solve By Elimination Method 1 X 3y 7 And X Y 5 2 8x 5y 9 And 3x 2y 4 3 3x Y 3 And 4x Y 8 Brainly In
ELIMINATION METHOD One of the unknowns with the same coefficient in the two equations is eliminated by subtracting or adding the two equations Then the answer of the first unknown is You should first solve the system by eliminating either x' or y' from the equation If you do that you get a trivial equation with the solution you mentioned Working with theAnswer (1 of 3) x/2 y/2 = 0 (×2) ====> x y = 0 (1) 3x/2 5y/3 = 7/3 (×6) ===> 9x 10y = 14 (2) (1)×10 10x 10y = 0 (3) (3) (2) x = 14
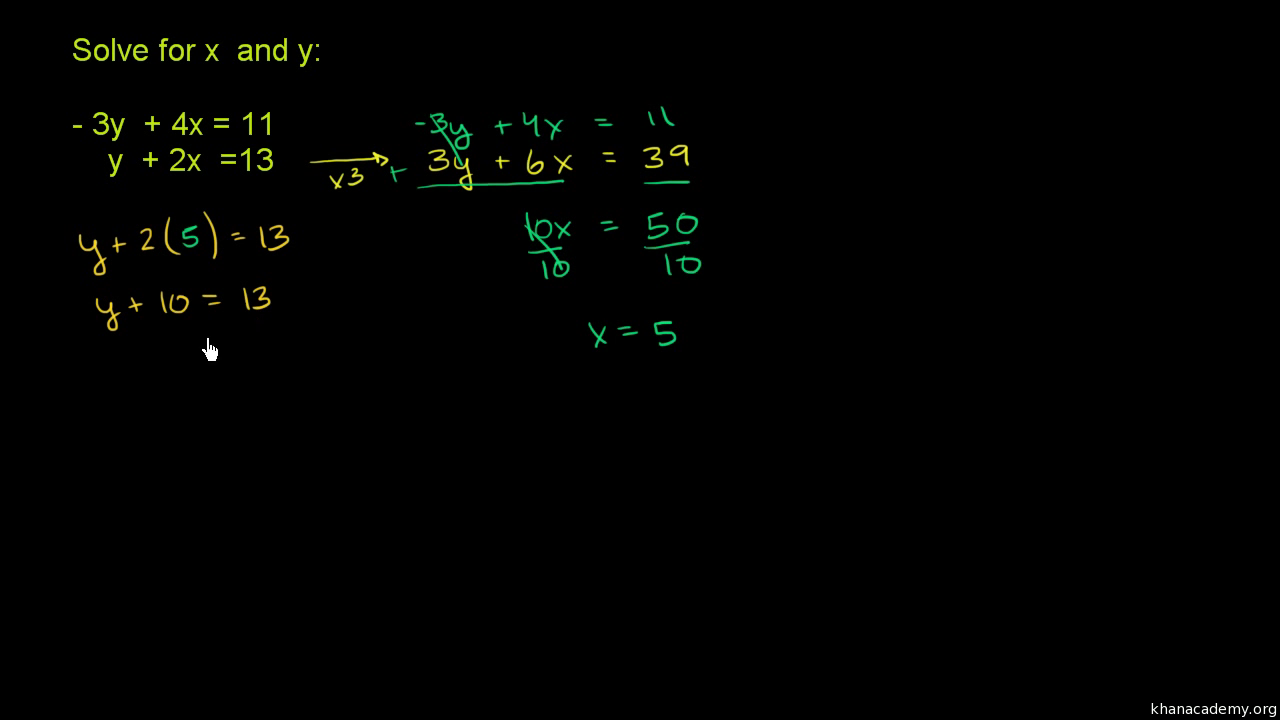



Systems Of Equations With Elimination 3y 4x 11 Y 2x 13 Video Khan Academy



How To Solve For X And Y In X Y 5 And Xy 6 Quora
Free system of equations elimination calculator solve system of equations unsing elimination method stepbystep This website uses cookies to ensure you get the best experience By usingElimination Method Steps Step 1 Firstly, multiply both the given equations by some suitable nonzero constants to make the coefficients of any one of the variables (either x or y) numerically equal Step 2 After that, add or subtract one equation from the other in such a way that one variableSolve by Addition/Elimination x2y=3 2x3y=9 x − 2y = 3 x 2 y = 3 2x − 3y = 9 2 x 3 y = 9 Multiply each equation by the value that makes the coefficients of x x opposite (−2)⋅(x −2y) =



Solved Find The Common Solution Of Each Using The Elimination Course Hero




Solved Solve The Following System Of Linear Equations Using The Gauss Jordan Elimination Method For The Variable X 4y 32 0 Zx 9y 42 2 3x 13y 72 2 No Solution
The elimination method for solving systems of linear equations uses the addition property of equality You can add the same value to each side of an equation So if you have a system x – 6How do you solve using the Gauss elimination method yz=2, 2x3z=5, xyz = 3?Or click the example About Elimination Use elimination




Solved Systems Of Linear Equations Eleination Method Chegg Com



If X Y 3 X Y 1 Then What Is X Y Quora
The steps of elimination method are 1) Select the variable to eliminate (it can be either variable) 2) Make the absolute value of coefficient for the variable selected (for elimination) is the sameNow, the step is eliminating the variable y in both the equations (2) and (3) as given below and finding the value of x When you do so, you get, 2x y = 750 x y = 548 __________ x = 2Elimination x2y=2x5, xy=3 \square!




X Y 4 2x 5y 1




Substitution Method X Y 5 And 2x 3y 4 Youtube
The simultanous equation calculator helps you find the value of unknown varriables of a system of linear, quadratic, or nonlinear equations for 2, 3,4 or 5 unknowns A system of 3 linear equations Solving Systems Of Equations By Elimination Method Step I Let the two equations obtained be a 1 x b 1 y c 1 = 0 (1) a 2 x b 2 y c 2 = 0 (2) Step II Multiplying the givenExample 2 Using the elimination method of solving linear equations find the values of 'x' and 'y' 3x y = 21 (1) 2x 3y = 28 (2) Solution By using the elimination method, let us




Solved Activity 1 What Am I Direction Using The Slope And Y Intercept Identify Whether The System Of Equations Are A Consistent And Independent B Consistent And Dependent Or C Inconsistent Write The Letter
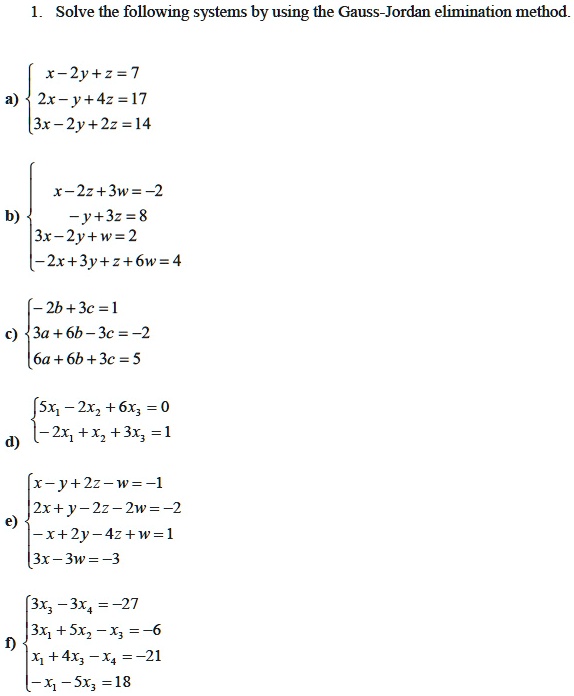



Solved Solve The Following Systems By Using The Gauss Jordan Elimination Method X 2y Z 7 2x Y 4z 17 3x 2y 2z 14 R 2z 3w 2 Y 3z 8 Bx 2y W 2 2r 3y Z 6w 4 2b 3c 1 3a 6b
These are the elimination method steps to solve simultaneous linear equations Let us take an example of two linear equations xy=8 and 2x3y=4 to understand it better Let, xy=8 ___ (1) and 2x3y=4 ___ (2) Step 1 To make the coefficients of x equal, multiply equation (1) by 2 andSolve by elimination method 2x 5y = 127x 3y = 13 Easy View solution > Solve each of the following pairs of equations by the elimination method 2 x 3 y = 8 4 x 6 y = 7 Easy View Ex 34, 1 (Elimination)Solve the following pair of linear equations by the elimination method and the substitution method (i) x y = 5 and 2x – 3y = 4 x y = 5 2x – 3y = 4



How To Solve Using The Gauss Elimination Method Y Z 2 2x 3z 5 X Y Z 3 Quora




3 2 Warm Up Solve The System Graphically 4x 2y 8 X Y 1 5 4 3 2 5 4 3 2 X 2y 8 4x 2y 4x 8 Y 2x 4 X Ppt Download
Steps Download Article Write down both of the equations that you'll need to solve Number the equations 3x y = 12 as number one, and 2x y = 13 as number two Check if bothUse elimination to solve the system 2xy= 12 −3xy= 2 2 x y = 12 − 3 x y = 2 Show Solution You can eliminate the yvariable if you add the opposite of one of the equations to the other Gauss Elimination method x y =2 and 2x 3y = 5 Get the answers you need, now!




Ex 3 4 1 I Class 10 Solve By Elimination And Substitution




Elimination Method Day 1 Ppt Download
The elimination method of solving systems of equations is also called the addition method To solve a system of equations by elimination we transform the system such that one variableSolution Solution provided by AtoZmathcom Elimination Method Solve Linear Equation in Two Variables Solve linear equation in two variables 1 12x 5y = 7 and 2x 3y 5 = 0 2 x y = 2Step 1 1 of 3 2 x 6 y = 17 − ( 2 x − 10 y = 9) 2x6y=17 (2x10y=9) 2 x 6 y = 17 − ( 2 x − 10 y = 9) 16 y = 8 16y=8 16 y = 8 y = 1 2 y=\frac {1} {2} y = 2 1 subtract the second equation from



If X Y 3 X Y 1 Then What Is X Y Quora
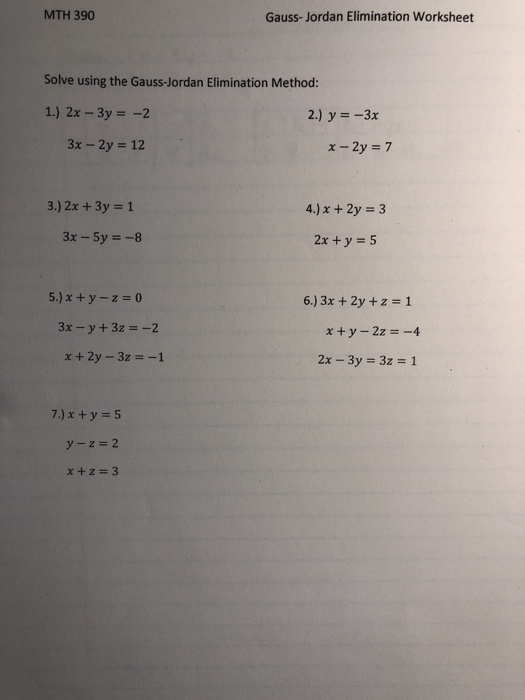



Solved Mth 390 Gauss Jordan Elimination Worksheet Solve Chegg Com
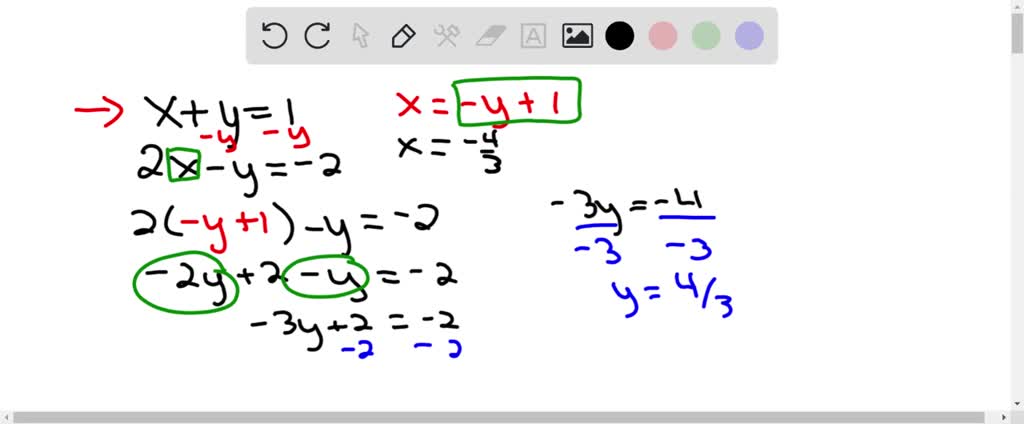
3 => 2x = 4 x = 2 The solutions are x = 2 and y = 1 Graphical Method In this method, two straight lines are drawn for each equation Then the point where the two lines intersect at isClick here👆to get an answer to your question ️ Solve the equations using elimination method 2x y = 2 and x y = 4Use the elimination method to solve the system 7x 2y =12 2x 3y = 4 7 8 (2x y = 6 4x6y=8 9 (5x7y=13 3x = 1 2y Use the substitution method or the elimination method to



How To Solve Using The Gauss Elimination Method Y Z 2 2x 3z 5 X Y Z 3 Quora




Series 575 552 533 518 507 500 A Find The Value Of A
Numerical Analysis Multiple Choice Questions & Answers (MCQs) on "Gauss Elimination Method 1 Solve the following equations by Gauss Elimination Method Hence, x = 2 Find theMohdaarif3259 mohdaarif3259 Math Secondary School answered Gauss EliminationGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!



Solved Solve Each System Using The Substitution Method Begin Array C X Y 1 2 X Y 2 End Array




Solved Solve The Following System Of Linear Equations By Chegg Com
Solve this linear system using the elimination method 2x 3y = 4 3x – 2y = 6 Multiply the first equation by 2 and the second equation by 3, and then add them together to clear the equations By adding the two equations together you eliminate the y variable which allows you to solve x = 6 Alternately, subtract one equation form the other eliminating the x and allowing y =The trick with Gaussian elimination is to find the leading element (circled) at from the starting matrix and new



Solving Simultaneous Equations The Substitution Method And The Addition Method Algebra Reference Electronics Textbook




Solved Solve The Following Systems Of Equations State Whether The System Is Consistent Or Inconsistent As Well As Dependent Or Independent 3x 6y 2 5x 4y 1 Using Substitution Method
Hours ago Example 2x^2=18 dominant specifies that a dominant test of genotypic association tests are to be performed 0015 # # P value adjustment bonferroni method for 2 tests # TestsIn order to use the elimination method, you have to create variables that have the same coefficient—then you can eliminate them Multiply the top equation by 5 5 5 ( 3 x 4 y) = 5 (




Solve 2x Y 5 And 3x 2y 8




Solved Exercises Use The Suhstitution Method To Solve Each System Of Linear Equations 1 X Y 3 2 Y 2x 3 Y 3x X 7 2y 3x Y 10 Sx Zy



Using Matrices Solve The Following System Of Equations 2x 3y 5z 11 3x 2y 4z 5 X Y 2z 3 Quora




Solve The Following System Of Linear Equations Of Graphically X Y 1 2x Y 8 Brainly In
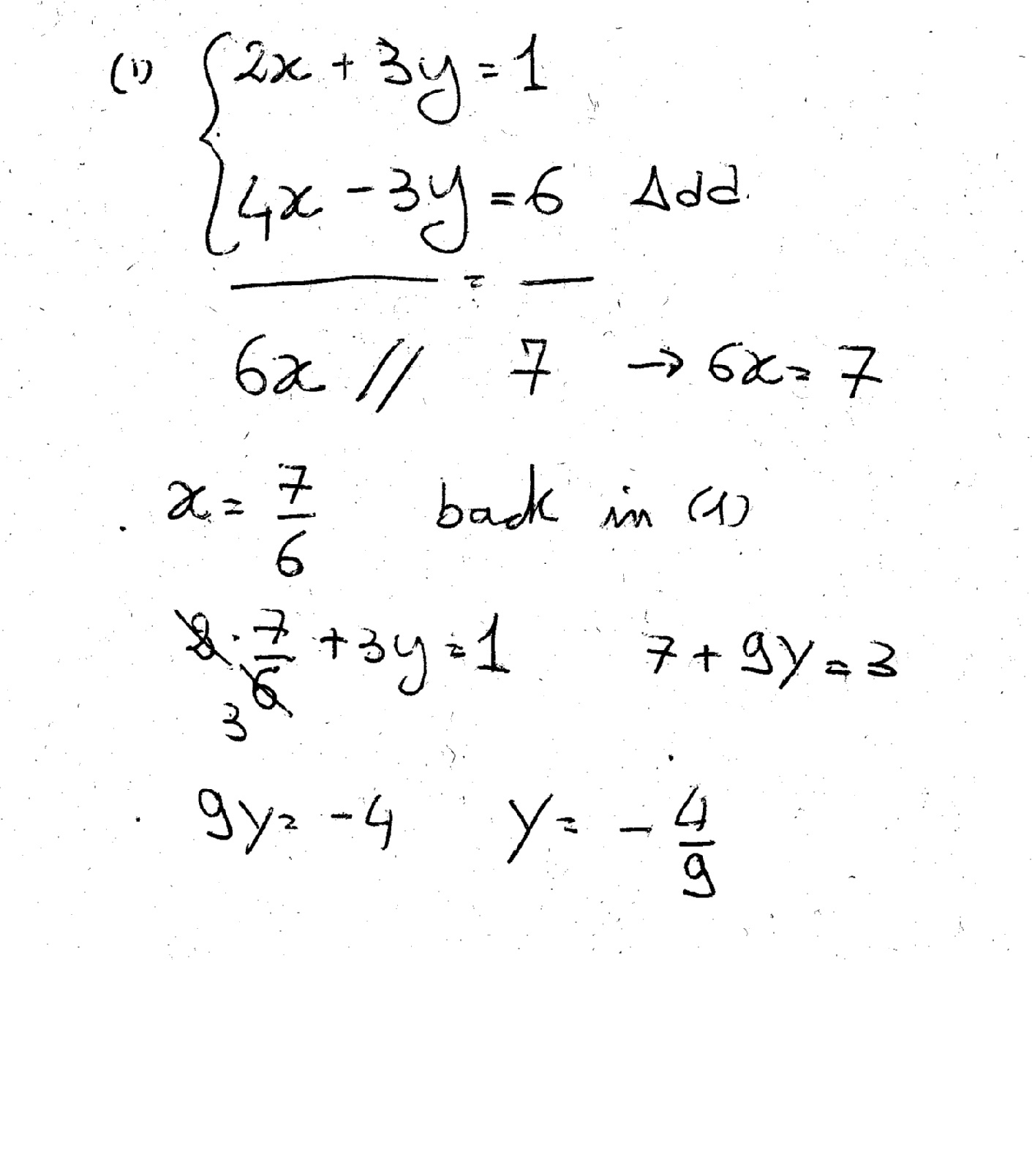



How Do You Solve The System Using The Elimination Method For 2x 3y 1 And 4x 3y 6 Socratic




Solve The Following System Of Equations 27 X Y 15 X Y 2 And 30 X Y 1 X Y 3 Mathematics Topperlearning Com X68shsoo



How To Solve The Simultaneous Equations X 2y 7 2x Y 1 Quora




2x X Y 6 2 X 2x Y 3 1 Mathematics Topperlearning Com Fqktm544



1




Solve X Y 2 2x 3y 5 Brainly In



3 Y 10 Sale 56 Off Www Hcb Cat




Math 163 Online Problems Supplemental Lessons On Gaussian




Solved 8 Find The Inverse Of A 3 9 Solve The Following Chegg Com




Solve For X And Y Using Substitution Method 2x Y 7 4x 3y 1 0 Youtube




Solve 2x Y 1 X Y 2 By Elimination Method Brainly In




Chapter 8 Problems




Solve For X And Y By Elimination Method X Y 8 2x 3y 1 Brainly In




Solve The Following Systems Of Equations 2x 3y 1 60x 40y 19 X 0 Y 0




Elimination Method X Y 5 And 2x 3y 4 Youtube




Elimination Method Day 1 Ppt Download



1




2x Y 4 0 X Y 1 0 Graphically Mathematics Topperlearning Com C02j6uyy




2x 3y 2 X Y 2 1 2 Practice Set 1 3 Crammers Method क र मरच पद धत Crammers Rule Grade 10 Youtube




Solve The Following Pair Of Linear Equations By The Elimination Method And The Substitution Method X Y 5 And 2x 3y 4




Solve The Following By Elimination Method 2x Y 6 And X 2y 2



Systems Of Linear Equations
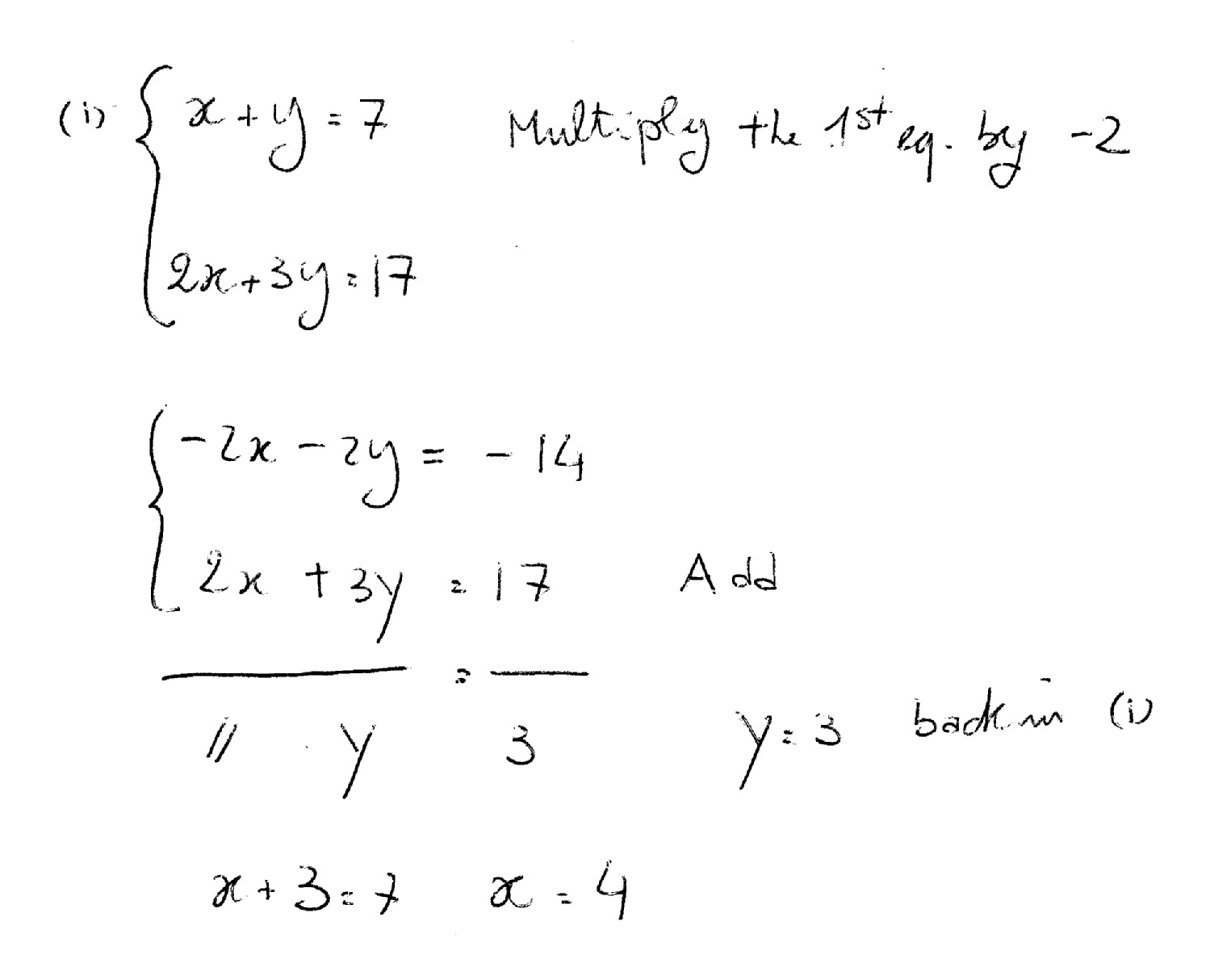



How Do You Solve The System Using The Elimination Method For X Y 7 And 2x 3y 17 Socratic




Solve Each Other Pair Of Equation Given Below Using Elimination Method 3 X 2 Y 9 Xy 9 X 4 Y 21 Xy Mathematics Topperlearning Com 59bn37qq




Ex 3 6 1 I And Ii Solve 1 2x 1 3y 2 1 3x 1 2y




Solved Solve The Following System Of Linear Equations Using The Gauss Jordan Elimination Method For The Variable Y X Y 3x 2y 0 2x Y 4 No Solution Y 2 Y
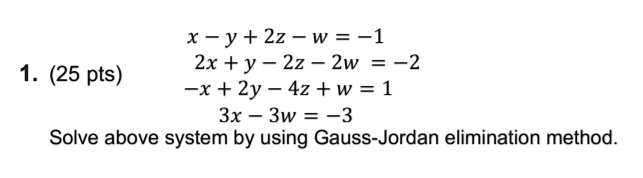



Solved X Y 2z W 1 2x Y 2z Zw 2 X 2y 42 W 1 3x 3w 3 1 25 Pts Solve Above System By Using Gauss Jordan Elimination Method




Solved Solve The System Graphically And By Hands X 2 Y 2 Chegg Com
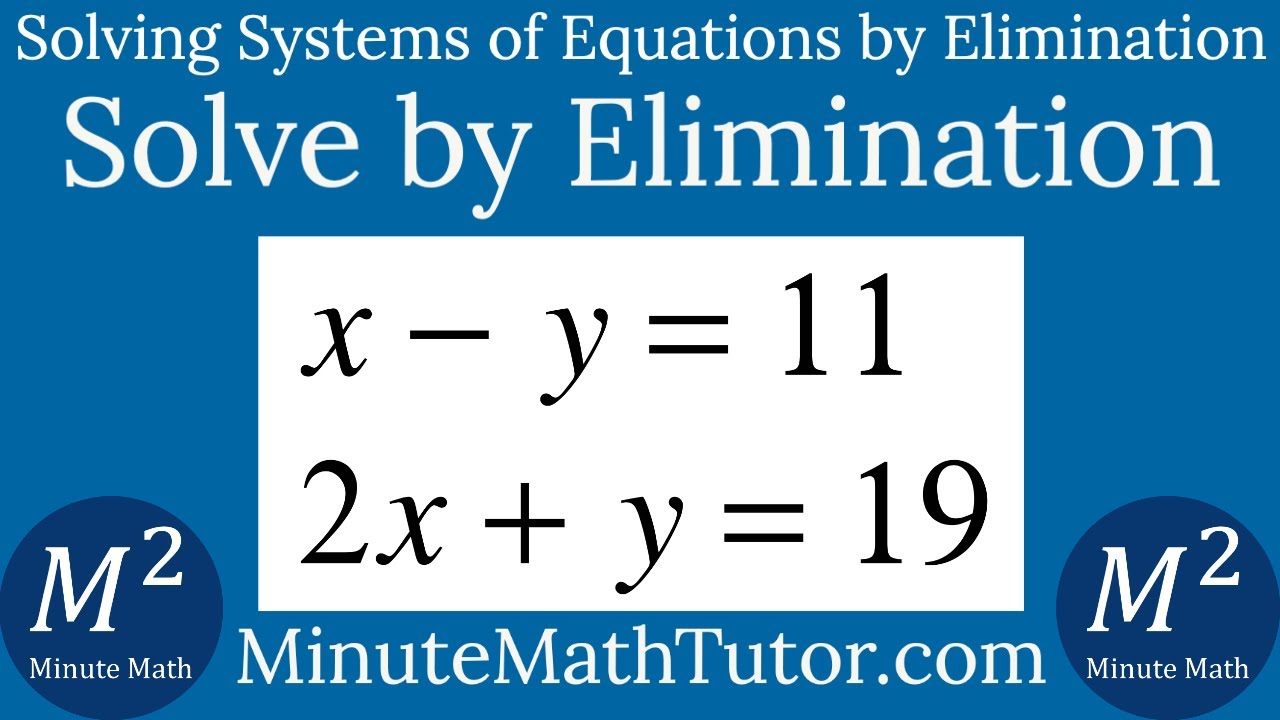



Solve X Y 11 And 2x Y 19 By Elimination Youtube



How To Solve The Following Simultaneous Equations By Elimination Method A 2x 3y 12 X Y 1 B 3x Y 10 C X 3y 1 3x 2y 4 0 D 5 Quora




Solve Each With Substitution 2x Y 6 Y 3x 5 3x 4y 4 Y 3x Ppt Download




Elimination Method Definition Steps Examples




J19




Notes 2 13 Addition Method Of Solving A System Of Equations Also Called The Elimination Method Ppt Download




Solve The System X Y Z 6 X Y Z 2 2x Y Z 1 Using Matrix Inverse Youtube




Solved Use Gaussian Elimination Method To Solve The Chegg Com




Use The Elimination Method To Solve The Following Systems Of




Solve The Pair Of Linear Equations X Y 1 And 2x 3y 2 By Elimination Method Brainly In




2x Y 11 And X Y 8 Solve Using Substitution And Elimination Method Youtube



1




Solved Find The Inverse Of A 3 9 Solve The Following Systems By Using A Gauss Elimination Method And B Cramer Rule X Y Z 2 2x Y Z 0 Xt2y 2 4 Ii Zy 3z 2



How To Solve Simultaneous Equations Using The Elimination Method 3x 2y 8 And 4x Y 7 Quora




3 2 Warm Up Solve The System Graphically 4x 2y 8 X Y 1 5 4 3 2 5 4 3 2 X 2y 8 4x 2y 4x 8 Y 2x 4 X Ppt Download




X Y 1 And 2x Y 8 By Elimination Method Brainly In




Solve For X And Y 40 X Y 2 X Y 5 And 25 X Y 3 X Y 1 Mathematics Topperlearning Com Idbi1itt




Solved I Solve The Following System Of Linear Equations Chegg Com



How To Solve X Y Z 2 2x 3y 4z 14 5x 2y 3z 10 In Elimination Method Quora




Slove By Substitution Method X Y 2 2x Y 1 Brainly In




Solved In Exercises 17 36 Use The Gauss Jordan Elimination Chegg Com




X Y 14 X Y 4 Solve Using Elimination Method Youtube




How Do You Solve X Y Z 2 2x Y Z 5 And X 2y 2z 1 Using Matrices Socratic




3 Y 10 Sale 56 Off Www Hcb Cat



Solve The Following Systems Of Equations 3 X Y 2 X Y 2 9 X Y 4 X Y 1 Sarthaks Econnect Largest Online Education Community




Solved Solve The Following Systems Of Linear Equations By Chegg Com




2x Y 11 0 And X Y 1 0 By The Method Of Eleminaton Brainly In




Systems Of Equations With Elimination X 2y 6 4x 2y 14 Video Khan Academy




Solve 3x Y 2x Y 2 9x Y 4x Y 1




Solve The Following Systems Of Equations X Y 2 And 2x 2y 4 Brainly In



If 2x 3y 17 And 3x 5y 27 What Are X And Y Quora




2x X Y 6 2 X 2x Y 3 1 Solve The Equation Brainly In




Solve These By Elimination Method 1 2x Y 4 And 5x 3y 1 2 Maths Pair Of Linear Equations In Two Variables Meritnation Com




Ex 3 4 1 I Class 10 Solve By Elimination And Substitution




Example 12 Use Elimination Method 2x 3y 8 4x 6y 7




7 2 7 3 Solving By Substitution And Elimination Ppt Video Online Download




2x 3y 12 And X Y 1 Problem Set Q3 1 Linear Equation In Two Variables Algebra Class 10th Youtube




3 Y 1 Hot Sale 60 Off Www Emanagreen Com




Solved Direction Solve The Following Systems Of Linear Equation Using Elimination Method 2x Ty 40 2x 3y 3r 4y 7 10 2r Y Ix Y 7 11 X Y 13 X 2y 12 X Y 5




X 2 2y 3 1 And X Y 3 3 Find X And Y Values Using Elimination And Substitution Method Youtube



The Elimination Method




Solve By Elimination Method X Y 5 2x 3y 5 Brainly In




Solved 5 41 5 0 6 30 Solve Each System Using Gaussian Chegg Com
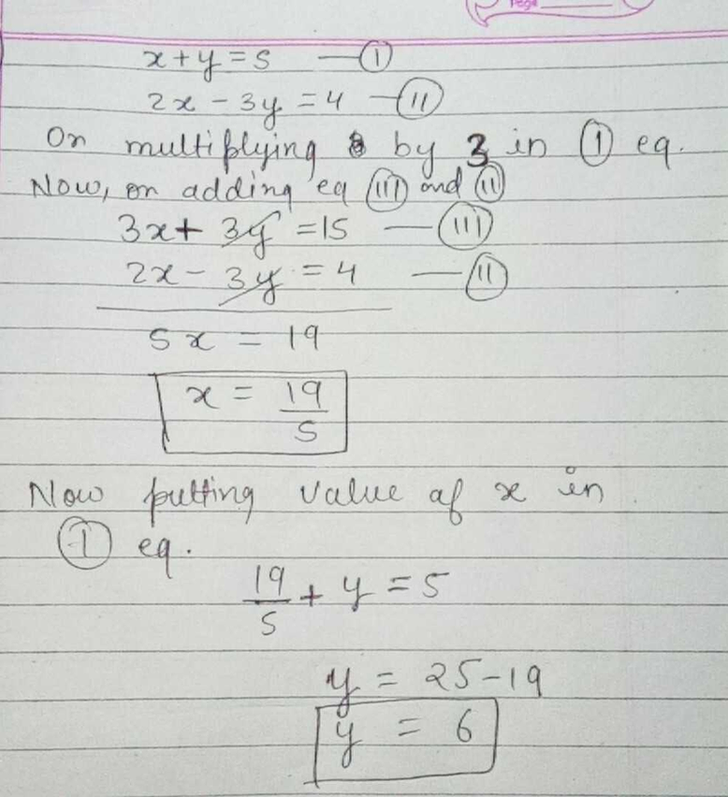



X Y 5 And 2x 3y 4 By Elimination Method Scholr




Solved Solve The System Of Linear Equations By Using Chegg Com



0 件のコメント:
コメントを投稿